Math Students Gain Invaluable Experience Exploring Symmetry in Summer Research Program
Most people are aware of the many ways in which symmetry can appear in the world around
us, be it in art, architecture, nature, or geometry. Far fewer of us, however, have been exposed to how symmetries can be used to help solve problems in mathematics. Last summer, two SOU mathematics students, Will Helman and Daniel Sinderson, embarked on an undergraduate research project through SOU’s Summer Research Experience program to do just that. However, instead of studying the symmetries of triangles or squares (or any other shape for that matter), their project focused on studying the symmetries of an important class of equations in math and physics called differential equations.
Differential equations allow us to relate how quantities change with respect to one or more variables. Nearly all important physical phenomena, from the humble falling apple to the supermassive black holes of general relativity, are modeled with differential equations. Naturally then, mathematicians and physicists alike have devoted an immense amount of effort to their analysis. Despite these efforts, very little is actually known about solving differential equations. In fact, for most differential equations, we have no standard techniques for finding solutions, even if we can prove solutions exist.
In the late 1800s, the Norwegian mathematician Sophus Lie discovered that if a differential equation has enough symmetry (transformations which leave the equation unchanged), then those symmetries can be exploited to rewrite the equation in a simpler form, possibly leading to its solution. From then on, mathematicians have been concerned, not only with finding the solutions to differential equations, but also with trying to analyze what symmetries an equation might possess.
The so-called classical symmetries studied by Lie were expanded upon in the 1960s by mathematicians Bluman and Cole. These new nonclassical symmetries were shown to always contain the classical symmetries. However, they could also lead to solutions that the classical symmetries might miss.
The project, led by Dr. Brandon Ashley of the SOU Mathematics Department, analyzed the classical and nonclassical symmetries of two physically relevant differential equations: the Born-Infeld (BI) equation of relativistic string theory:
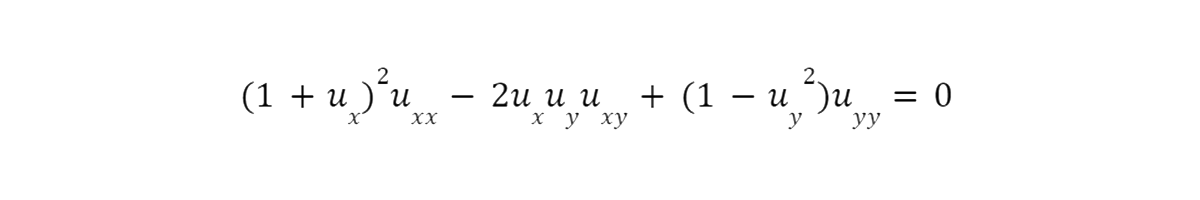
and the Reduced Gibbons-Tsarev (RGT) equation of dispersionless systems:
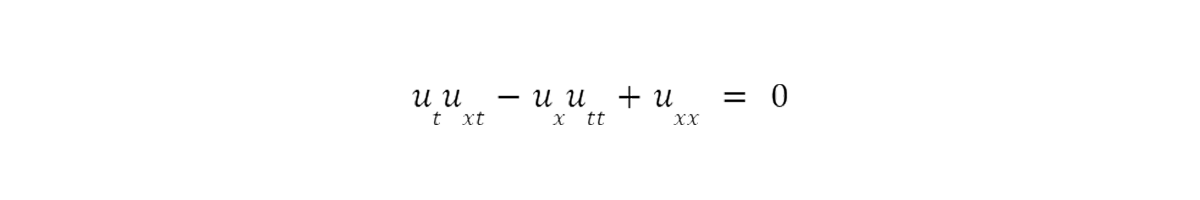
In earlier work, Dr. Ashley was able to show that both of these equations have special properties which allow them to be transformed to especially simple, linear equations, but it was unclear whether or not these transformations could be detected using either classical or nonclassical symmetry methods. Will and Daniel were tasked first with learning the general theory behind the classical and nonclassical symmetry methods and then with calculating the classical and nonclassical symmetries of the BI and RGT equations to see what connections could be made.
*Spherical Representation of Solutions to the Born-Infield Equation
Despite the impressively difficult calculations involved (even when aided by the mathematical software Maple), Will and Daniel were able to show that the set of classical symmetries and the set of nonclassical symmetries for the BI and RGT equations were precisely the same, respectively. Will and Daniel’s results naturally lead one to wonder if the special properties of the BI and RGT equations could have been used to predict the so-called classical equals nonclassical phenomenon and in particular if every equation whose classical symmetries match the nonclassical symmetries will have these special properties.
These questions and others are currently being addressed by Dr. Ashley’s on-going research with talented SOU students like Will and Daniel. When asked about their summer research experience, Will and Daniel had the following to say:
“Summer research with Dr. Ashley was a rewarding experience. Of course, math research is nothing like math class. While investigating your problem, it’s easy to become lost in associated questions you will invariably meet along the way. In (especially lower division) math classes, if a question occurs to you, it’s likely that it has come to many other students before you at the prompt of such well-explored material. When you dive into higher-level topics, chances are that no one has ever wondered what you are wondering. It can be daunting. During Dr. Ashley’s crash course, very natural questions occurred to Daniel and me, and increasingly they were met with “no one knows,” “that’s still an open question,” or a shrug and chuckle. It was extremely exciting. When it came time to tackle the research problem, the feeling that we were on untrodden grounds remained. Ultimately, one of those questions proved to be the biggest takeaway from the project, and it has big implications.
We got a taste of theoretical math research, and used specialized computational techniques for our problem. We learned a little differential geometry and Lie theory to do it. The experience was a blast, and solidified my excitement about my future career in research.”
“It was a huge privilege to be able to work on the project this summer with Will and Dr. Ashley. At the start, I expected it would largely be a pen and paper project involving some proofs. Instead, it was a massive computational project involving a computer algebra system and the scariest looking equations I’ve yet seen.
We started learning background material for the project in late June. The crash course Dr. Ashley took us through was difficult but well-taught, and it covered both the computer algebra system we used (navigation, programming, and the documentation of some specialized modules we used) and the actual mathematics behind the project including methods for solving problems that, beforehand, would’ve been literally impossible for me to solve. These were the hard skills learned in the project.
The soft skills are what really stand out to me though. It turns out math research is hard. And much different than math classes. I’m 35. I’ve been thrown (or jumped) into at least half-a-dozen projects I’m barely prepared for, but this was the first time I’ve truly doubted if I was up to the task and had to push through. Easily 95% of my working time was spent stuck and churning through failed attempts at a solution. To go through that experience well-supported and then come out the other side with solutions in hand (and a fascinating direction for future research thanks to Will!) was a very rewarding experience. It’s one that I honestly didn’t expect to be available to me at a small regional university like SOU. I’d do it again and would recommend the experience to other students in the department in a heartbeat.”
The generous support of donors was essential to the success of the Summer Research Experience. In particular, the Allan and Katherine M. Alsing Fund for STEM Research provided 23% of the funding while numerous donors to the STEM Division Fund for Excellence provided 52% of the funding. The balance came from SOU program funds and allowed for the funding and support of this research by Dr. Ashley, Daniel, and William.
